Concave vs. Convex (Definitions, Differences, Examples)

What’s the difference between concave vs convex? Keep reading to learn the difference!

What’s the difference between concave vs convex?

Concave and convex are words that describe the shape of objects. A concave shape describes the surface that curves inwards, whereas convex shapes describe surfaces that curve outwards, like a sphere or a round ball.

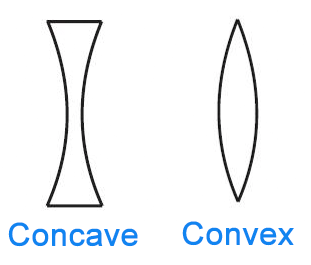
Concave and convex are both adjectives that describe the shape and curvature of objects, i.e., nouns.

For example, the inside of a bowl or a spoon have surfaces that are concave, and curve inwards. Therefore, these objects can be described as ‘concave’ in shape.

Concave shapes are thinner in the middle than they are at the edges; whereas convex shapes have a thicker middle and are usually thinner at the edges.

A basket ball, for example, or car tires, are two common objects that have a convex shape, since both objects curve outwards rather than inwards.

How to remember the difference between concave vs convex

A mnemonic to the rescue! As a quick aside, mnemonics are little learning techniques to use that help to retain information.

Here’s one to help remember the difference between concave and convex.

A quick tip to remember the difference!

The word concave has the word cave in it: caves are hollow spaces that form naturally in the earth, or on the side of a cliff or mountain. Caves curve inward, and so they are concave.

• Concave = cave = go in the cave, (since it goes inwards.)

Convex curves outward, think of the two last letters, ex, as exit meaning out or external.

• Exit = convex = exit the cave (exit goes out; convex goes outwards.)

This simple trick albeit obscure tip should hopefully help to recall the difference between the two words, and their opposite meaning’s.

Convexdescribes the exact opposite shape of concave. Convexcurves outward and are rounded outward; examples of objects that are convex includes a rugby ball or basketball.

Concave vs. convex lenses

In daily life, concave and convex can be used to describe the curve of glass surfaces, such as eyeglasses, or the shape of eyeglass lenses. That said, in everyday speech and conversation, these words are not commonly used because they are more formal and technical terms (usually reserved for mathematics or science subjects.) See the following use cases of both words:

Concave and convex lenses are both used depending on whether people are nearsighted or farsighted.

Concave lenses are thicker at the edges than at the center. Concave lenses disperse light rays which makes things appear farther away. People that have difficulty seeing things up close would use concave lenses, since they are nearsighted.

• The side mirror of a car has a concave surface.
• Binoculars have concave lenses.

A convex lensdome outward and are thicker in the middle than they are around the edges. Convex lenses are the opposite of concave: they make things look closer or bigger rather than farther or smaller.

Magnifying glasses, certain eyeglasses, microscopes and some binoculars have convex lenses.

Concave and convex polygons

In geometry, the words concave and convex describe different shapes of polygons. Polygons are shapes that have a flat surface and straight lined edges.

In Greek, poly means many and gon means angles. Its name is quite literal: many angles.

Polygons have a minimum of three sides, and can have up to any number of sides or straight-lined edges. Polygons are named based on the number of sides they contain, as shown in the image below.

See the image below showcasing different types of polygons.

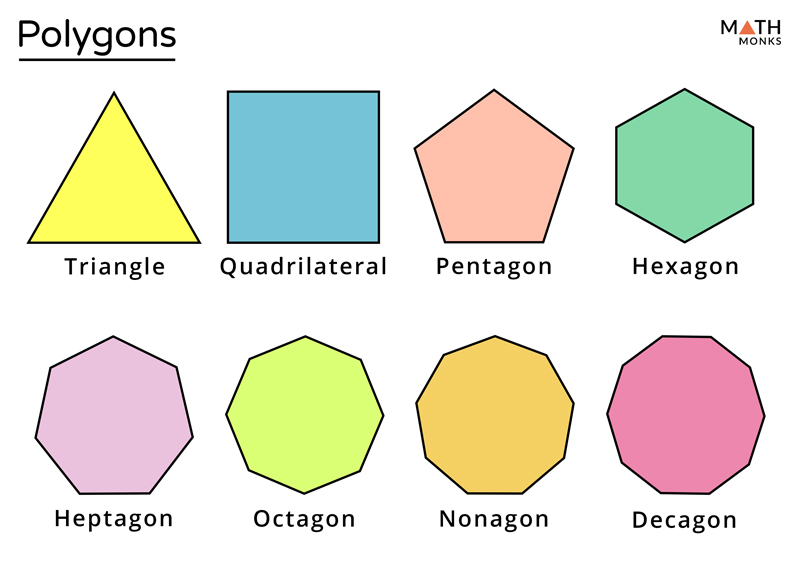
Another way to classify polygons is based on their side lengths. Based on their angles and the angle degree, polygons either fall under the category of convex polygons or concave polygon; i.e., a non-convex polygon.

A convex polygon has all its interior angles at less than 180°.

Examples: Triangles, all convex quadrilaterals, a regular pentagon, and a regular hexagon are all convex polygons. A square is also a regular convex polygon.

A concave polygon, also known as a non-convex polygon, must have one of its interior angles measure more than 180°. Concave polygons are irregular polygons since its interior angles are different measures; whereas convex polygons can have both regular and an irregular shape.

Concave and convex functions

Concave and convex also refer to functions in math.

According to Wikipedia, a concave function is “The negative of a convex function. Concave functions are also synonymously called concave downwards, concave down, convex upwards, convex cap, or upper convex.”

Also according to Wikipedia, a “real-valued function is called convex if the line segment between any two points on the graph of the function lies above the graph between the two points.”

Whatever that means! this is Grammar Brain not Math Brain. Apologies for the lacklustre explanation on the math functions, but there are surely websites that cover both convex functions and concave in depth.

To learn more about a convex function and how it works, it’s probably best to speak with a math teacher or tutor.

Concave and convex mirrors

What’s the difference between concave and convex mirrors? Mirrors are super smooth surfaces that project images by reflecting the light.

There are two main types of mirrors: plane mirrors and spherical mirrors. Plane mirrors and spherical mirrors are divided into convex and concave mirrors.

Both mirrors reflect extremely different images in their reflection. A convex mirror is bent outwards and looks somewhat bulging; whereas a concave mirror faces inward.

Concave mirrors makes the reflection appear larger whereas with convex mirrors what’s reflected appears smaller.

Examples of concave vs. convex in a sentence

Look at the following examples of sentences that use concave and convex

1. We manufacture convex lenses for various purposes, including telescopes and binoculars.
2. The convex surface of a magnifying glass lens is what produces magnification.
3. Most of the basic polygons that you’re familiar with are convex polygons, including triangles, rectangles, pentagons, hexagons, and octagons.
4. Many cameras use both concave lenses and convex lenses to provide the ability to zoom in and out.
5. The description said the car has “several concave surface features”—which was a misleading way of saying “dents.”
6. The telescope has a large convex mirror to collect the light.
7. The graph of a concave function is always below its tangent.
8. A convex lens is used to concentrate rays of light.
9. The doctor told me to use convex lenses to improve my sight.
10. The palm of one’s hand is somewhat concave .

Example sentences are from dictionary.com.

Origin of the word concave

Concave comes from the early 15c., Old French concave (14c.) or directly from Latin concavus, meaning “hollow, arched, vaulted, curved,”

“From con-, here perhaps an intensive prefix (see con-), + cavus “hollow” (from PIE root *keue- “to swell,” also “vault, hole”).” (from etymonline.com.)

Origin of the word convex

“Curved like a circle or sphere when viewed from outside,” 1570s, from French convexe, from Latin convexus, “vaulted, arched,” past participle of convehere “to bring together,” from assimilated form of com “with, together,” or “thoroughly” (see com-) + vehere “to bring, carry, convey” (from PIE root *wegh- “to go, move, transport in a vehicle”).

In Review

• Concave surfaces curve inward.
• Convex surfaces curve outward.

Glossary

1. Definition of concave
2. Definition of convex

Sources

1. Example sentences on using concave vs convex
2. Polygon images
3. Concave versus convex image
4. Image of cave by Devon Janse van Rensburg on Unsplash